А.А. Соловьев [0000-0002-4376-1120]
Географический факультет МГУ имени М.В. Ломоносова, Москва, Россия
E-mail: a.soloviev@geogr.msu.ru
Аннотация. Анализируются методы описания механических и электродинамических систем с неголономными связями. Выявляется роль выбора счета времени при описании динамики систем с голономными и неголономными связями. Рассматривается возможность перехода от уравнений механики к аналогичным уравнениям электродинамики для силовых энергетических полей с измененным мероопределением времени.
Ключевые слова: счет времени, голономные, неголономные связи, уравнения Лагранжа.
1. Введение
В последние годы активизируется интерес к механике сплошных сред, электродинамике, квантовой механике систем со связями, допускающими ограничения на изменения, как обобщенных координат, так и обобщенных скоростей [1]. Такие связи по Г.Герцу [2] принято называть неголономными, в отличие от голономных связей, зависящих только от обобщенных координат. Для механических систем с неголономными связями общие уравнения механики по причине взаимной зависимости координат не приводят к уравнениям Ж.Лагранжа, свойственных системам с голономными связями. С.А.Чаплыгин показал, каким образом в результате преобразований времени можно получить уравнения движения неголономных систем, аналогичные уравнениям Лагранжа [3]. Вслед за этим начались исследования с использованием разнообразных подходов, приводящих к преобразованию уравнений движения неголономных систем в различные формы [4]. В современных исследованиях неголономных систем отмечается обилие публикаций по различным задачам неголономной динамики большинство, из которых восходит к развитию работы С.А.Чаплыгина. В числе других подходов к описанию неголономных систем отметим работу А.С. Предводителева, который обратил внимание на значимость использованного при выводе уравнений С.А. Чаплыгина приводящего временного множителя [5]. Согласно которому при описании механических систем с неголономными связями можно принять постулат о переходе к другому исчислению времени. Аналогичные идеи преобразования времени реализуются в развитии метода расчета динамических полей неголономно связанных структур [6]. С этим же связаны исследования, в которых развивается нетрадиционный подход к задачам неголономной механики и электродинамики с переходом от эвклидова пространства к метрике пространства Лобачевского Римана [7].
Основу таких подходов, нередко не укладывающихся в общепринятые представления, как правило, составляет сравнительный анализ между понятиями различных областей науки. Тем не менее к сравнительным аналогиям все же продолжаются обращаться для лучшего понимания нового явления. Но не только для этого, а потому, что нередко при всем несходстве явлений их описание сводится к абстракциям, в своем математическом выражении почти тождественно повторяющим друг друга. Получается так, что, хотя явления физически разнородны, а математические алгоритмы сближают их до уровня достаточно близкого соответствия. И это происходит от того, что у каждого положения одной теории существует гомолог в другой. Поэтому задачи, решенные в одной из них, могут быть использованы в другой. Этот факт позволяет не только формально отображать одну область знания в другую, но и взаимно ускорять их развитие. Аналоги являются проверенным инструментарием, позволяющим в новом явлении усмотреть старое с дополнением новых качеств [5, 8].
Представленные суждения являются преамбулой представляемой далее статьи, иллюстрирующей возможности аналогий для распространения алгоритмов, разработанных для решения задач динамики механических систем с голономными связями, на другие системы, которые оказались в силу ряда причин неприемлемыми для систем с неголономными связями.
2. Определение времени в механике точек с неголономными связями
Мы привыкли к расчетам времени в механике настолько, что не задумываемся над тем, как происходит выбор единицы изменения времени при описании того или иного физического явления. Между тем, этот вопрос в первую очередь должен быть однозначно решен при постановке той или иной задачи. В механике в качестве образцового движения выбирается прямолинейное и равномерное движение, с которым сравниваются все остальные. Тем самым принимается, что выбор способа измерения течения времени в классической механике определяется однозначно. При построении электродинамики, выбор счета времени по образу классической механики не годится. Принято считать, что для того, чтобы уравнения электродинамики не зависели от выбора координат, а это необходимо, счет времени должен осуществляется в соответствии с группой преобразования Лоренца-Эйнштейна [9].
Но и в механике, как оказалось, далеко не всегда возможно пользоваться ньютоновским мероопределением времени. Уравнения Лагранжа для движения материальных точек, свободного с голономными связями, так составлены, что при мероопределении времени можно без уточнений пользоваться равномерным и прямолинейным движением как образцовым, с которым допустимо сравнивать все другие. Но этого сделать нельзя, если механическая система подвержена неголономным связям. В этом случае уравнения Лагранжа изменяют свой вид. Чтобы сохранить его необходимо специально выбрать счет времени в зависимости от характера неголономных связей. Именно это главная идея описания процессов в неголономной механике, на которую как на весьма важное и принципиальное положение указал впервые С.А.Чаплыгин [3]. Для пояснения значимости этого положения обратимся к рассмотрению его примера механической системы с двумя свободными обобщенными координатами q1 и q2. Будем считать, что зависимые параметры, определяемые координатами x,y материальных точек системы, подчиняются следующим условиям
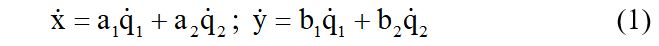
Здесь множители, a1, a2, b1, b2 суть, произвольные функции параметров q1, q2, а x, y, q1, q2 обозначают производные по времени от всех параметров. Уравнения движения системы в форме Лагранжа для данного примера получаются из принципа Даламбера, и они для кинетической энергии Т и потенциальной энергии U запишутся так:
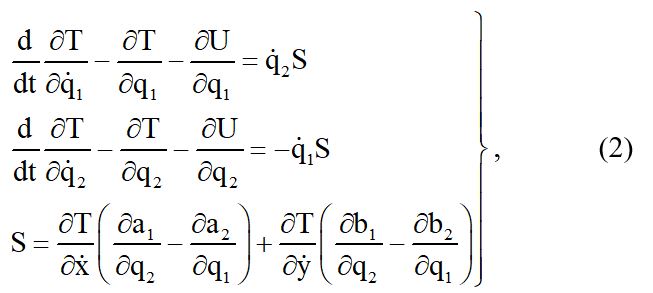
Эти уравнения отличаются от обычных уравнений Лагранжа членом S в правой части. Он будет равен нулю только в случае интегрируемости уравнений связи (1).Но оказывается всегда можно найти такое преобразование течения времени от единиц t к единицам τ, которое позволяет написанную систему уравнений движения свести к обычному виду уравнения Лагранжа. С этой целью С.А.Чаплыгин рекомендует принять следующий формат преобразования времени через множитель М ,считая его некоторой функцией независимых переменных q1, q2.

По смыслу введения коэффициент М является множителем, переводящим один счет времени в другой. После преобразования приведенных выше уравнений к новому течению времени τ, получаем уравнения:
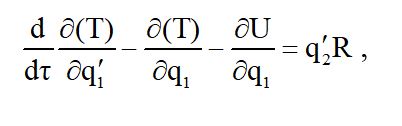
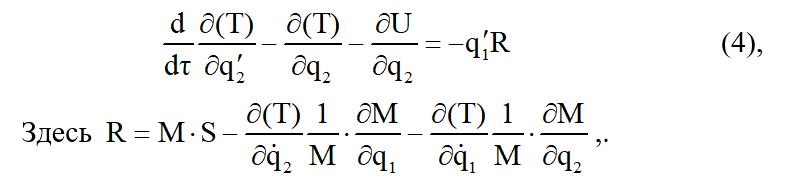
а производные по новому времени τ обозначены штрихами q1, q2 ,скобки в этих равенствах означают, что кинетическая энергия (Т) берется в преобразованном виде, например.
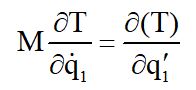
Очевидно, что приводящий множитель М можно выбрать так, что при этом параметр R обратится в нуль, т.е. когда:
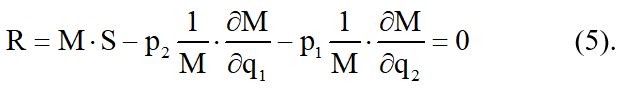
Здесь введены следующие обозначения
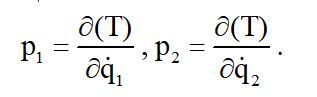
Итак, мы видим, что с помощью уравнения (5) можно уравнения (4) привести к обычному виду уравнений Лагранжа, т.е. всегда существует приводящий множитель М, позволяющий подобрать такой счет времени, который дает возможность использовать уравнение механики в форме уравнений Лагранжа.
3. Время в статистических системах с неголономными связями
Полученный результат с приводящим множителем для механических систем имеет первостепенное значение и для статистических систем, подверженных действию неголономных связей. Покажем, что для таких систем подбор способа измерения времени с использованием приводящего временного множителя М приводит к необходимости пользоваться теоремой Лиувилля в исправленном виде. Проанализируем доказательство этой теоремы с использованием уравнений Гамильтона, которые по существу являются лишь видоизменением уравнений Лагранжа.
Пусть U — потенциальная, а T — кинетическая энергия, W — полная энергия системы. Уравнения движения в каноническом виде такой системы можно записать следующим образом:
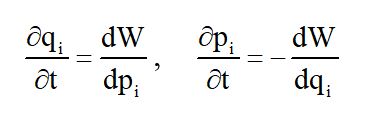
Здесь q — обобщенные координаты, p — обобщенные импульсы. К этим уравнениям для вполне определенного движения следует еще присоединить условия относительно начальных координат, импульсов и времени, которые в дальнейшем будут обозначаться штрихами.
Но можно поступить иначе, а именно начальные координаты, импульсы и время рассматривать как независимые переменные. И написать систему дифференциальных уравнений относительно 2n + 1 этих независимых переменных. С этой целью следует воспользоваться интегралом действия
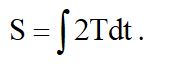
Этот интеграл будет некоторой функцией координат q и W.
В аналитической механике [4] доказывается, что
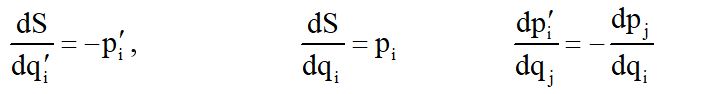
К этим уравнениям присоединяются еще следующие соотношения
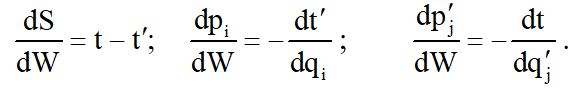
Пользуясь этими уравнениями можно установить следующую связь между начальным и конечным значением фазового элемента:
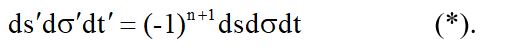
Здесь введены такие обозначения:
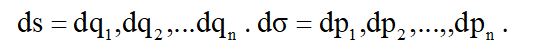
Принимая, что течение времени можно выбирать произвольно, то можно принять равенство начального и конечного значения времени dt’ = dt. Тогда из равенства (*) следует ds’dσ = dsdσ. В том случае если система подвержена неголономным связям, то уравнения Лагранжа, а, следовательно, и уравнения Гамильтона следует писать относительно переменной с новым счетом времени τ, а не с прежним t. Но поскольку для единиц измерения времени dτ’ и dτ по отношению к dt’ и dt существуют соотношения Чаплыгина , определяемые приводящим множителем М, то :

В этом случае между фазовым элементом и его начальным значением для измененного мероопределения времени будет иметь место следующая зависимость:
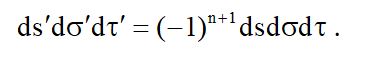
Поэтому имеем:
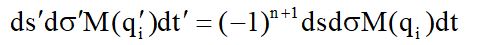
Так как dt’ = dt, то это приводит к такому равенству начального и конечного значения фазового объема согласно теореме Лиувилля
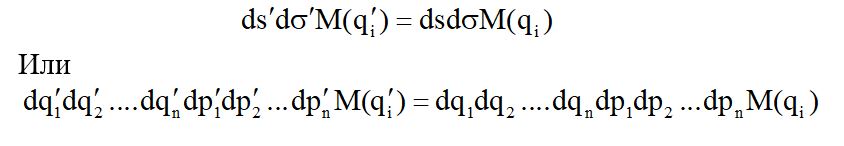
С учетом того что имеет место равенство M(q’) = M(q), после несложных вычислений можно получить следующее соотношение для функции распределения числа частиц находящихся в фазовом объеме :
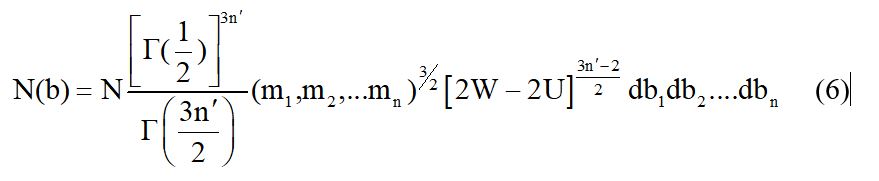
Здесь величины (m1 … mn) являются массами частиц;. N(b) выражает число частиц статистической системы, заключенных в фазовом объеме db1 … dbn, тогда как моменты могут иметь любые значения, совместимые с уравнением энергии.
Символом Гобозначена гамма -функция, символ n’ обозначает число материальных частиц в системе, поэтому имеем: n=3n’.Для числа систем с конфигурацией (b), для которых один из моментов, например, pn заключен в интервале a и an + dan, получаем :
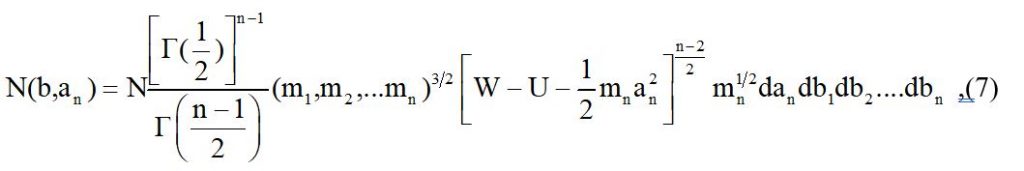
Зная два числа систем по соотношениям (6)и (7) легко найти меру числа таких систем, для которых pn лежит между b и an + dan.
Эта мера будет совпадать с функцией распределения. Итак, будем иметь
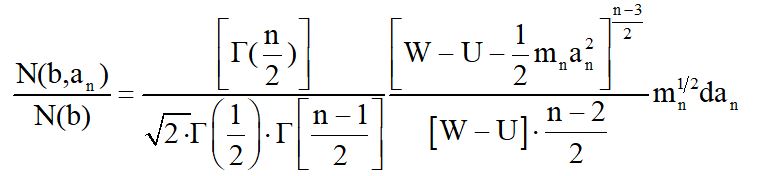
Из приведенного краткого изложения вывода распределений Максвелла явствует, что только в одном случае функция распределения останется неизменной для неголономных систем. Именно, тогда, когда при интегрировании отношение M(qi)/M(q’i) получает одинаковое значение в обеих формулах (4)и(5).
4. Электродинамическая аналогия уравнений движения материальной точки с неголономными связями общего типа
Выше велись рассуждения о движении материальной точки с неголономными связями при условии, когда в линейных уравнениях связей отсутствовал свободный член. Посмотрим, как изменятся уравнения Лагранжа для неголономных связей следующего типа
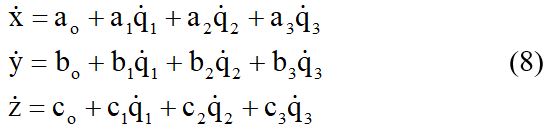
Обобщим написанные уравнения и в другом смысле. Будем считать, что производные в этих уравнениях относятся не к течению времени по Ньютону, а к течению времени, измеряемому с помощью функции t’ = t'(t).
Тогда уравнения (8)по отношению к течению времени по Ньютону можно переписать так:
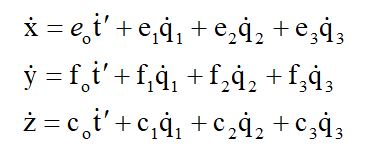
Уравнения Лагранжа для рассматриваемой задачи можно получить, исходя из принципа Даламбера.
Опуская несложные математические выкладки, запишем только окончательный результат:
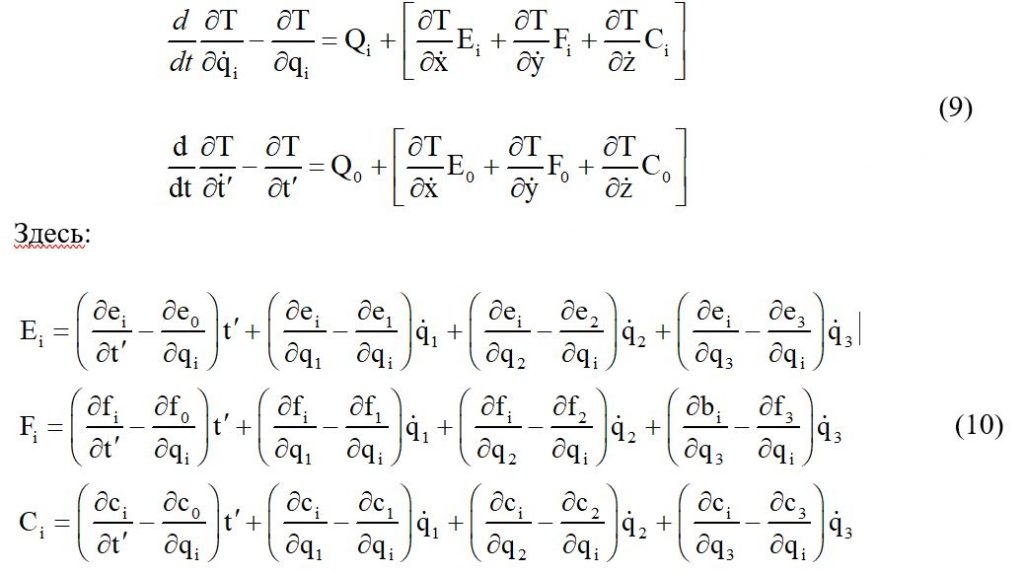
Уравнения (9) вместе с тождествами (10)являются решением поставленной задачи. Полученные уравнения движения материальной точки с неголономными связями можно обобщить на любую систему материальных точек.
Уравнения Лагранжа будут справедливы и для системы точек с неголономными связями, если постоянные ei, fi, ci и e0, f0, c0 выбраны так, что обращают в нуль выражения в квадратных скобках в уравнениях (9). Это будет тогда, когда коэффициенты при производных в тождествах (10) обращаются в нуль. Но в этом случае связи становятся интегрируемыми.
Рассмотрим один частный вид неголономных связей; именно положим
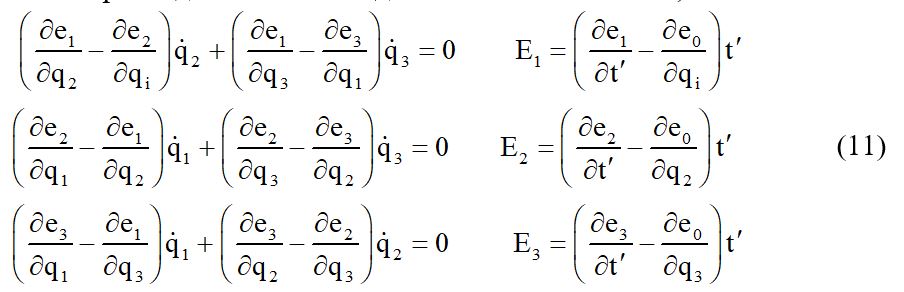
Кроме этих соотношений должны быть справедливы еще два соотношения с производными по t’ именно:
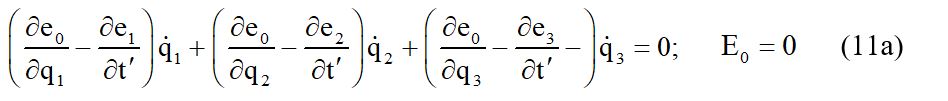
Cоотношения алогичные составленным для функций можно записать и для функций fi, fo, ci, c0. Если значения величины Ei рассматривать, как компоненты вектора электрической напряженности, значения величин ei как компоненты векторного потенциала электромагнитного поля, а скалярную функцию e0 как скалярный потенциал электромагнитного поля , то одну группу из равенств (11) можно записать в векторном виде так:
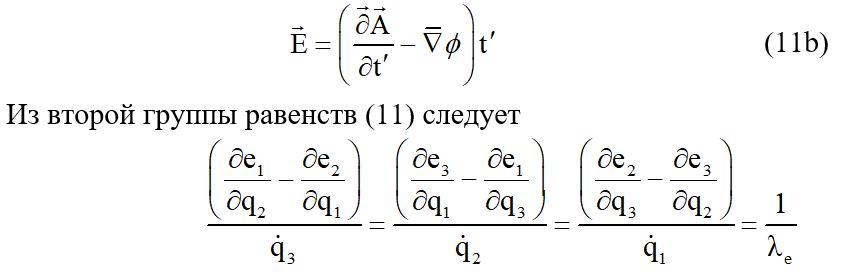
Здесь через λ обозначена некоторая постоянная. Последнее равенство можно записать в виде одного векторного равенства, если величины q рассматривать как компоненты вектора q = H, который в общепринятых обозначениях соответствует вектору напряженности магнитного поля H. Тогда последнее равенство, представляя вектор e как векторный потенциал А можно записать так

Полученные уравнения (11b) и (11c) аналогичны уравнениям Максвелла, выраженным через векторный А и скалярный ϕ потенциалы. Аналогия будет совершенно полной, если производную t’ приравнять постоянной величине 1/c.
5. О множителях, сводящих электромагнитную аналогию к тождеству
Допустим, что существует такой множитель μе, который превращает уравнения (11b) и (11c) в уравнения Максвелла, т.е. положим, что имеют место такие равенства:
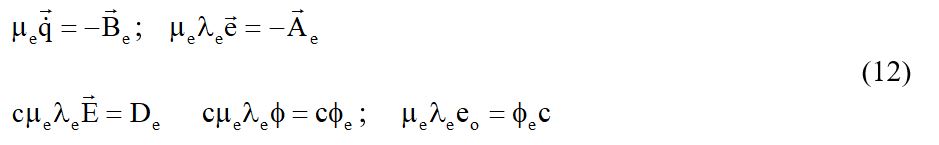
При этих условиях уравнения (11b) и (11c) переходят в следующие:
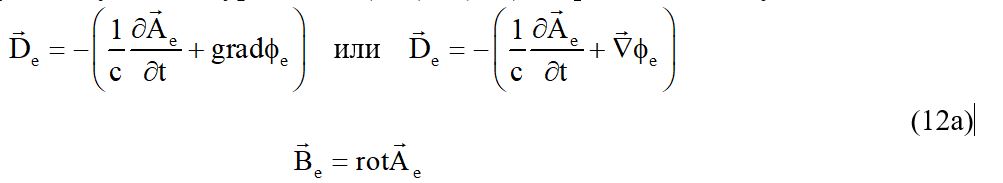
Здесь принято во внимание также условие ct’ = t.Существование условия (11а) позволяет утверждать, что вектора D и B взаимно ортогональны.;
Подобные уравнения можно написать и для функций f и с.Таким образом, неголономные связи в форме дифференциальных уравнений (9) могут играть роль анизотропного поля Максвелла.
Однако, ограничимся частным случаем изотропного поля, когда имеют место равенства:
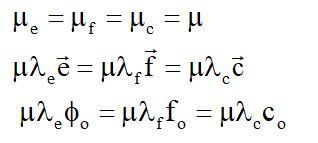
Эти равенства вместе с условиями (12) позволяют уравнения для неголономных связей (8) представить в следующем виде:
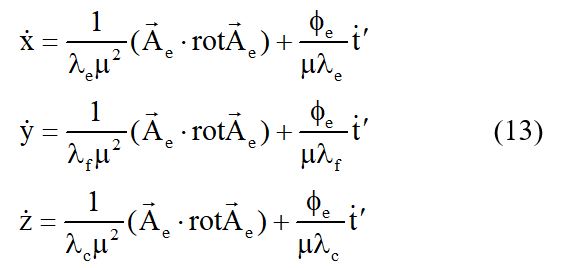
С помощью найденных уравнений для неголономных связей формула для преобразований кинетической энергии будет выглядеть так:

Из этого соотношения можно вывести ряд любопытных следствий. В частности, при выбранном варианте неголономной связи, характерном для электромагнитных систем типа электрических генераторов с ветровыми ресурсами возобновляемой энергии [10] для описания процессов электрогенерации можно использовать аналог уравнения Лагранжа с параметрами
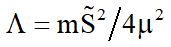
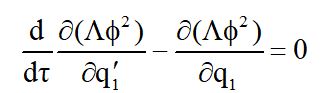
Это означает, что расчет параметров генерации электрической энергии электромагнитной системы с неголономными связями удовлетворяет решению модифицированного уравнения Лагранжа, с кинетической энергией, определяемой T потенциалом электродвижущей силы. В целом полученные результаты свидетельствуют о том, что видоизмененные аналоги уравнений неголономной механики в случае неголономных электродинамических систем могут быть использованы для формирования общих подходов к теоретическому рассмотрению инновационных технологий возобновляемой энергетики.
6. Заключение
Несмотря на ограниченные возможности метода сравнительных аналогий физически различных явлений, которому не стоит придавать большого значения. Тем не менее, в некоторых частных случаях, о чем свидетельствуют приведенные расчеты, следует обращаться к уточнениям выбора счета времени для преобразования неголономных систем различной физической природы к аналогам динамических уравнений Лагранжа в видоизмененной форме. Представленные результаты следует рассматривать как часть исследований направленных на объединение аналитических методов механики и электродинамики применительно к расширенному описанию нелинейных энергетических процессов.
Литература
- Manuel de León A historical review on nonholomic mechanics// 2012 Revista de la Real Academia de Ciencias Exactas, Físicas y Naturales. Serie A, Matemáticas (RACSAM) V.106,P.191–224. (DOI: 10.1007 / s13398-011-0046-2)
- Hertz, H., Gesammelte Werke: Vol. 3. Die Prinzipien der Mechanik, Leipzig: Barth, 1894.
- Чаплыгин С.А. Исследования по динамике неголономных систем. М.-Л.: ГИТТЛ,1949-112 с.
- Alexey V. Borisov, Ivan S. Mamaev, Ivan A. Bizyaev Historical and critical review of the development of nonholonomic mechanics: the classical period| //Regular and Chaotic Dynamics. 2016, volume 21, P.455–476.(DOI:10.1134/S1560354716040055).
- Предводителев А.С. Математический счет и наше познание // История и методология естественных наук , 1965 , вып.3,Физика.С.13-152.
- Подосенов С.А. Пространство, время и классические поля связанных структур. _ М.: Спутник 2000 -.445 с.
- Подосенов С.А., Потапов А.А., Фоукзон Дж., Менькова Е.Р.Неголономные, фрактальные и связанные структуры в релятивистских сплошных средах,
- электродинамике, квантовой механике и космологии: Кн. 2. М.: Издательство Ленанд, 2016 .- ,440 с.
- Макки, С. Практические инструменты для новых идей / С. Макки // Intelligent Enterprise/. 2004. №5. — С.24-26.
- Мёллер К. Теория относительности, М.: Атомиздат, 1975.
- Неймарк Ю. И., Фуфаев Н. А. Динамика неголономных систем. М.: Наука, 1967.
Reference
- Manuel de Leоn A historical review on nonholomic mechanics// 2012 Revista de la Real Academia de Ciencias Exactas. Fisicas y Naturales. Serie A. Matematicas (RACSAM) V.106.P.191–224. (DOI: 10.1007 / s13398-011-0046-2)
- Hertz. H.. Gesammelte Werke: Vol. 3. Die Prinzipien der Mechanik. Leipzig: Barth. 1894.
- Chaplygin S.A. Issledovaniya po dinamike negolonomnykh sistem. M.-L.: GITTL.1949-112 s.
- Alexey V. Borisov, Ivan S. Mamaev, Ivan A. Bizyaev Historical and critical review of the development of nonholonomic mechanics: the classical period| //Regular and Chaotic Dynamics. 2016, volume 21, P.455–476.(DOI:10.1134/S1560354716040055).
- Predvoditelev A.S. Matematicheskiy schet i nashe poznaniye // Istoriya i metodologiya estestvennykh nauk . 1965. vyp.3.Fizika. S.13-152.
- Podosenov S.A. Prostranstvo. vremya i klassicheskiye polya svyazannykh struktur. _ M.: Sputnik 2000 -.445 s.
- Podosenov S.A.. Potapov A.A.. Foukzon Dzh.. Menkova E.R.Negolonomnyye. fraktalnyye i svyazannyye struktury v relyativistskikh sploshnykh sredakh. elektrodinamike. kvantovoy mekhanike i kosmologii: Kn. 2. M.: Izdatelstvo Lenand. 2016 .- .440 s.
- Makki. S. Prakticheskiye instrumenty dlya novykh idey / S. Makki // Intelligent Enterprise/. 2004. №5. — S.24-26.
- Meller K. Teoriya otnositelnosti. M.: Atomizdat. 1975.
- Neymark Yu. I.. Fufayev N. A. Dinamika negolonomnykh sistem. M.: Nauka. 1967.
